Praprzodek, czyli wycieczka ku 16 bitom
Podróż przez rozszerzenia architektury procesorów x86 rozpoczniemy od
skoku w przeszłość. Pierwszy powszechnie znany komputer osobisty firmy IBM -
PC model 5150 - zbudowany został w oparciu o kość 8088. Był to funkcjonalny
odpowiednik 16 bitowego procesora 8086, lecz z przyciętą do 8 bitów szyną
danych - sama konstrukcja komputera stawała się przez to trochę prostsza, a
przy okazji można było zastosować tańsze, 8 bitowe elementy. Z punktu
widzenia oprogramowania procesory te różniły się jednak głównie prędkością
jego wykonywania. Możliwe były operacje tak na liczbach 8, jak i 16 bitowych
- zwanych słowami.

Praprzodek: pierwszy CPU komputerów IBM PC (źródło: Red Hill CPU Guide)
Kolejny przedstawiciel rodziny - 80186 - nie
zmienił zasadniczo modelu programowania. Układ ten integrował rdzeń
procesora z kilkunastoma układami pomocniczymi (m.in. zegarem, kontrolerami
DMA i przerwań), wprowadził też kilka nowych instrukcji, powszechnie
przypisywanych następcy - prawdopodobnie ze względu na nikłą obecność 186 w
komputerach PC. Rewolucyjne zmiany poczynił za to 80286 - wprowadzono nowy
sposób pracy - tryb chroniony. Niestety, wciąż 16 bitowy. Wymagania
użytkowników wciąż rosną - tak było i za tamtych, jakże odległych już
czasów. Programy stawały się coraz większe. Podział pamięci na bloki o
rozmiarze do 64 KB (216 bajtów), zwane segmentami, stawał się
największą kulą u nogi 286 - co z tego, że pamięci mogło być do 16 MB, jeśli
operowanie większymi strukturami było co najmniej niewygodne. Rozwiązanie?
Więcej bitów.
32 bity w rodzinie: 386

Intel 80386 - x86 goni konkurencję
Wielkie nadzieje wiązano z kolejnym układem Intela - 80386. Przy
zachowaniu wstecznej zgodności z 16 bitowymi poprzednikami, była to
konstrukcja w pełni 32 bitowa. Oznaczało to dostęp - przynajmniej
teoretycznie - aż do 4 GB ciągłej przestrzeni adresowej. Nowy, 32 bitowy typ
danych ochrzczono niezbyt fortunnym mianem podwójnego słowa. Intel
nie chciał wprowadzać zamieszania, i słowo pozostało liczbą 16
bitową, wbrew potocznemu rozumienia tego terminu - natywnego typu danych
procesora.
386 przyniósł ze sobą znacznie więcej - mechanizm stronicowania (podziału
pamięci na dosyć małe bloki - 4 KB) we współpracy z wbudowaną jednostką
MMU (ang. Memory Management Unit) umożliwiał realizację
wymiatanej na dysk pamięci wirtualnej. Także i instrukcje operujące na
bitach okazały się całkiem przydatne. Wprowadzono nowe tryby adresowania
pamięci, upraszczające pracę programisty. Dzięki temu linia x86 pierwszy raz
stała się faktycznie konkurencyjna wobec propozycji innych producentów.
Wszystko to działo się w połowie lat 80 ubiegłego wieku - spodziewać się
więc można dalszej ewolucji podstawowej architektury x86. Rzeczywistość
trochę jednak zaskrzeczała - szersze przyjęcie 32 bitowego oprogramowania
nadeszło dopiero ładnych parę lat później. Przez dłuższy czas kolejne
procesory - 486, ale też i Pentium - wykorzystywano po prostu jak
turbodoładowane odpowiedniki 80286. Stąd kolejna znacząca zmiana - 64 bitowe
rozszerzenia AMD64 - rozpoczęła się dopiero w roku 2003, wraz z
wprowadzeniem Opteronów.
A gdyby tak coś policzyć?
Właśnie - mowa tu o ewolucji procesorów, typach danych, etc. Ale jak w
praktyce wygląda styk program-procesor? Jak wyglądają instrukcje, które
wykonuje CPU? Przełamując strach przed asemblerem, postaramy się przebrnąć
przez obliczanie prostego wyrażenia arytmetycznego. Słyszę już głosy - po
co? Spokojnie - zobaczymy, jak z liczeniem poradzi sobie procesor klasy 386,
a później - gdy dojdziemy do mających w końcu być bohaterami tekstu
rozszerzeń - zobaczymy, co wnoszą w kwestii wykonania omawianego kodu.
Zajmijmy się zatem jednym z etapów obliczania pierwiastków równania:
ax2 + bx + c
W pewnym momencie obliczeń potrzebny będzie tzw. wyróżnik trójmianu -
oznaczany literą delta:
Δ = b2 - 4 ac
Wyrażenie to zapisane w języku wysokiego poziomu przyjmie postać:
b * b - 4 * a * c
Zobaczymy teraz, jaki kod zostanie wygenerowany przez kompilator.
89 da mov edx, ebx
0f af d3 imul edx, ebx
0f af c1 imul eax, ecx
c1 e0 02 shl eax, 0x2
29 c2 sub edx, eax
89 d0 mov eax, edx
Wygląda groźnie? Spokojnie - to wbrew pozorom proste. Spróbujemy policzyć
deltę dla równania 5*x^2 + 10*x + 4 (powinniśmy otrzymać w wyniku 20).
Zacznijmy od pierwszej instrukcji:
mov edx, ebx
Rozkaz ten (MOVe) służy
kopiowaniu wartości między pamięcią bądź rejestrami. Tutaj będziemy
mieli do czynienia wyłącznie z rejestrami ogólnego przeznaczenia. Te
zaś w przypadku procesorów zgodnych z 386 noszą nazwy eax,
ebx, ecx oraz edx.
Jaki więc będzie efekt wykonania pierwszej instrukcji? Wydawać się
może, że zawartość rejestru edx skopiowana
zostanie do ebx. Jest
inaczej - w składni firmy Intel, którą tutaj się posługujemy -
pierwszy argument to cel, a dopiero drugi - źródło. Instrukcja
ma więc postać:
mov dokąd, co
Pierwszy rozkaz przeniesie zatem zawartość rejestru ebx do
edx. Dlaczego? Co takiego kryje się w ebx? No tak, trzeba było
od tego zacząć - wartości zmiennych a, b oraz c
umieściłem - odpowiednio - w rejestrach eax, ebx, ecx. Zawartość
rejestrów wygląda więc po tym kroku tak:
| EAX = 5 | EBX = 10 | ECX = 4 | EDX = 10 |
Kolejna instrukcja:
imul edx, ebx
dokonuje mnożenia rejestrów (Integer MULtiply) edx oraz ebx
- podobnie jak w poprzedniej, tak i tu wynik zostanie zapisany
w rejestrze wymienionym jako pierwszy. 10 razy 10 daje 100, tak więc
tej liczby spodziewać się możemy wewnątrz edx:
| EAX = 5 | EBX = 10 | ECX = 4 | EDX = 100 |
Zauważmy, że tak naprawdę policzyliśmy kwadrat liczby b. Nie
powinien więc dziwić następny rozkaz:
imul eax, ecx
Wykonuje tu się kolejny krok obliczeń - liczba a
zostanie przemnożona przez c, wynik zapisany w eax:
| EAX = 20 | EBX = 10 | ECX = 4 | EDX = 100 |
We wzorze na deltę a * c wzięte jest cztery razy -
stąd kolejna instrukcja pomnoży zapewne zawartość rejestru eax.
Sprawdźmy to:
shl eax, 2
Czyżby nie? A jednak - rozkaz shl to przesunięcie
argumentu w lewo (SHift Left). To jakby dopisanie zer (tutaj dwóch)
na koniec liczby. W systemie dziesiętnym odpowiada to mnożeniu razy
10^2, lecz komputer działa w systemie dwójkowym - tutaj mnożymy
razy 2^2. Tak, tak - to właśnie oczekiwane przez nas działanie,
zapisane w szybszej postaci. Kompilatory stosują tą formę przy
mnożeniu przez potęgi dwójki. Jest jeszcze jeden powód, dla którego
nie wykorzystaliśmy ecx - to, że jest tam czwórka, jest
zasługą danych wejściowych - nasze c ma taką akurat
wartość. Spójrzmy, co mamy w rejestrach:
| EAX = 80 | EBX = 10 | ECX = 4 | EDX = 100 |
Hmm, pozostaje odjąć 4*a*c (teraz w eax) od b*b (aktualnie w
edx). Rozkaz odejmowania nosi nazwę sub (SUBtract), nie
powinna więc dziwić następująca konstrukcja:
sub edx, eax
| EAX = 80 | EBX = 10 | ECX = 4 | EDX = 20 |
Mamy wynik - 20! Ze względu na zastosowaną przez kompilatory konwencje, wynik należy
zwrócić przez rejestr eax:
mov eax, edx
| EAX = 20 | EBX = 10 | ECX = 4 | EDX = 20 |
Brawo - udało się dobrnąć końca analizy. Kod działa, ale jest z nim kilka problemów.
Pierwszy, którym się zajmiemy, to rodzaj przetwarzanych danych. Cały
czas mówimy o liczbach całkowitych - procesory x86, począwszy
od 8088, a na 386 kończąc - nie potrafiły przetwarzać liczb
zmiennoprzecinkowych. Do tego celu przeznaczone zostały osobne układy
- koprocesory numeryczne x87, którymi zajmiemy się w następnym
paragrafie. Problem drugi, innej natury - załóżmy, że mamy
policzyć dużą ilość delt. Jak to zrobić? Niestety, trzeba tyle razy
wywołać omówiony kod, ile jest danych do policzenia. Może da się
jakoś inaczej? Da się - ale to dopiero za chwilę.

Towarzystwo dla 8086 - koprocesor numeryczny 8087 (źródło: cpu-museum.com)
Latający przecinek

486 zintegrował CPU z FPU w ramach jednej struktury krzemowej
Nie ukrywajmy - liczby całkowite to nie koniec marzeń. Dosyć często przychodzi nam
zmierzyć się z problemem, w którym potrzebne będzie trochę więcej
precyzji. Możemy "podzielić" rejestr na część całkowitą i
ułamkową (ang. fixed point), nie daje to jednak takich
możliwości, jak użycie formatów zmiennoprzecinkowych (ang. floating
point). Stosowane powszechnie
formaty zgodne z normą IEEE-754 działają na innej zasadzie. Na
początek zastanówmy się nad wykładniczym zapisem liczby 324. Możemy
zapisać ją w kilku postaciach, przesuwając przecinek:
0,324 * 10^3
3,24 * 10^2
32,4 * 10^1
324 * 10^0
Zwykle stosuje się postać z jedną cyfrą przed przecinkiem, zwany notacją
naukową. Wystarczy zapamiętać tzw. mantysę (pole znaczące)
- 3,24, oraz wykładnik - 2, by w danym systemie
liczbowym odtworzyć konkretną liczbę. Dla systemu binarnego otrzymamy
wzór:
(-1)znak · mantysa · 2wykładnik
O dokładności zapisu liczby decyduje ilość bitów poświęconych mantysie.
Zmiana wykładnika powoduje jedynie przesunięcie przecinka - ot, zmienny
przecinek.
Liczba zmiennoprzecinkowa podzielona jest więc na trzy pola: bit
znaku, mantysę oraz wykładnik. Koprocesory x87 operują na trzech
formatach liczb:
|
typ liczby
|
ilość bitów
|
bity mantysy
|
bity wykładnika
|
|
single
|
32
|
23
|
8
|
|
double
|
64
|
52
|
11
|
|
extended
|
80
|
64
|
15
|
Formaty single oraz double, dzięki sprytnemu wykorzystaniu
specyfiki systemu binarnego, efektywnie dysponują dodatkowym bitem mantysy -
można uznać, że ma ona 24 lub 53 bity.
Gdzie koprocesor przechowuje liczby? Do tego celu wydzielono osiem 80
bitowych (zdolnych pomieścić liczby typu extended) rejestrów.
Niestety, zdecydowano się na utworzenie stosu. Nie ma więc
możliwości bezpośredniego wyboru danego rejestru - mamy do nich
dostęp jedynie względem wierzchołka, oznaczanego symbolicznie ST lub
ST(0). Wyższe numery oznaczają kolejne elementy stosu - od
ST(1) aż do ST(7). Naturalnie, wierzchołek przemieszcza się w czasie
obliczeń - jeśli w danym kroku obliczeń liczba była osiągalna
przez ST(2), to w następnym być może trzeba będzie użyć ST(3).
Zresztą, zobaczymy to na przykładzie. Naturalnie - delta.
dd 45 f0 fld [b]
dc 4d f0 fmul [b]
dd 45 f8 fld [a]
dd 05 50 85 04 08 fld [4]
de c9 fmulp st(1)
dc 4d e8 fmul [c]
de e9 fsubp st(1)
Dla uproszczenia - zamiast adresów pamięci - w nawiasach
kwadratowych podałem nazwy liczb, do których odwołują się instrukcje.
Rozpoczynamy od policzenia b*b - ładujemy b na
stos (fld - Floating poing LoaD):
fld [b]
Stos wygląda więc następująco:
Podnosimy
liczbę do kwadratu, mnożąc wierzchołek stosu przez b
(fmul - Fp MULtiply):
fmul [b]
Wynik trafia znów na wierzchołek stosu:
Ładujemy teraz a (równe 5), oraz stałą 4:
fld [a]
fld [4]
Stos będzie miał postać:
| ST(0): | 4 |
| ST(1): | 5 |
| ST(2): | 100 |
By otrzymać liczbę 100, musimy teraz odwołać się do trzeciego
elementu stosu - ST(2) - a jeszcze przed chwilą był to
wierzchołek (ST)! Następny fragment:
fmulp st(1)
to mnożenie ze zdjęciem ze stosu (Fp MULtiply and Pop).
Wykonane jest mnożenie ST(1)*ST(0), wynik zostaje zapisany w
ST(1), a ST(0) zdjęte ze stosu:
krok pierwszy (multiply):
| ST(0): | 4 |
| ST(1): | 20 |
| ST(2): | 100 |
krok drugi (pop):
fmul [c]
Kolejny rozkaz to zwykle mnożenie ST(0) * c, z wynikiem
umieszczonym na wierzchołku stosu:
Wreszcie ostatnia instrukcja odejmuje pozostałe liczby:
fsubp st(1)
Wynik odejmowania zapisany zostaje w ST(1), ale ponieważ chcemy też
zdjęcia wierzchołka stosu (forma Fp SUBtract and Pop), otrzymamy:
Pięknie - kolejny raz poprawny wynik. Zdążyliśmy zauważyć, że stos
potrafi zaciemnić obraz sytuacji. Co gorsza, większość instrukcji za
niejawny argument przyjmuje ST(0). Poważnie utrudnia to proces optymalizacji
oprogramowania - przynajmniej w porównaniu do maszyn o bezpośrednim dostępie
do rejestrów FPU. Co można zrobić, gdy chcemy dodać ST(1) do ST(5)? Jest
pewne rozwiązanie. Koprocesor oferuje instrukcję fxch (Fp
eXCHange), która zamienia zawartość wierzchołka z danym elementem stosu.
Można zatem zamienić ST(1) z wierzchołkiem, po czym wykonać operację
dodawania z elementem ST(5), by za pomocą kolejnego fxch przywrócić
kolejność danych na stosie. Otrzymujemy zatem funkcjonalność odpowiadającą
praktycznie bezpośredniemu dostępowi do rejestrów. Powstaje pytanie - jakim
kosztem? Jak długo wykonuje się fxch? Do procesorów 486 włącznie
trwało to dłuższą chwilę. Ale począwszy od Pentium fxch stało się
praktycznie "bezpłatne" - równolegle można było wykonywać inną operację FPU.
Do czasu - w Pentium 4, ze względu na poważne cięcia w obszarze koprocesora,
znowu trzeba się liczyć z kosztami wykonania fxch. Pech.
Tak oto dochodzimy do końca możliwości oferowanych przez klasyczną
architekturę x86. Podsumujmy - mamy możliwość wykonywania operacji na
liczbach całkowitych, a dzięki koprocesorowi - także i w formacie
zmiennoprzecinkowym. Póki co to tyle - przenieśmy się teraz do roku 1997 -
roku premiery procesora Pentium z rozszerzeniami MMX.
Trzy magiczne litery - MMX

Pentium MMX: nadeszła era SIMD
MMX był pierwszym rozszerzeniem architektury x86, które miało na celu
poprawę własności "multimedialnych" tychże procesorów. Intel wyczuł
dokonującą się rewolucję w sposobie korzystania z komputerów, rozpoczynający
się boom na intensywne medialnie aplikacje. Stąd pomysł na zestaw
MMX. By zająć się jego działaniem, musimy poznać kolejny skrót -
SIMD. Akronim ten rozwija się do angielskiego określenia Single
Instruction - Multiple Data. Oznacza to pracę nie z jedną daną, jak do
tej pory, ale z ich zestawem - jedna instrukcja (SI) obrabia na raz
wiele danych (MD). Dotychczasowy model pracy określić można jako
SISD. Weźmy dla przykładu dodawanie dwóch wektorów liczb - A oraz B,
obu długości czterech elementów. Klasyczna architektura wymagać będzie tylu
właśnie rozkazów, po jednym na każde pole wektora:
add A[1], B[1]
add A[2], B[2]
add A[3], B[3]
add A[4], B[4]
Dla odmiany w modelu SIMD dysponujemy zazwyczaj rozkazami wykonującymi
operacje równoległe (parallel).
Równoległe dodawanie nazwijmy padd:
padd A, B
Ta jedna instrukcja wykona taką samą pracę, jak cztery poprzednie. Na
tym właśnie polega idea przetwarzania SIMD - jeśli procesor
dysponuje odpowiednimi zasobami wykonawczymi, dodawanie trwać będzie
do czterech razy krócej! Pomysł ten też przyświecał konstruktorom
Pentium MMX.
Zauważmy ciekawy fakt - by wykonać operację na całym wektorze,
potrzebujemy rejestrów, w których przechowamy całe A, a także pełną
zawartość B. Procesory rodziny 386 (486, ale również Pentium Classic i
Pentium Pro) nie przewidują odpowiednio szerokich rejestrów - 32 bity to
trochę za mało by osiągnąć satysfakcjonujący poziom zrównoleglenia
przetwarzania. Powstała więc konieczność dodania nowych rejestrów, a wraz z
nimi nowych typów danych, na których pracować będzie jednostka MMX.
Przyjrzyjmy się im.

AMD K6 - MMX stalo sie standardem
Pentium MMX wprowadza 8 prawie-że-nowych rejestrów 64 bitowych.
Skąd takie określenie? Otóż okazuje się, że rejestry te pokrywają się z
rejestrami FPU. Od początku więc wiadomo, że konieczne będzie przełączanie
między kodem FPU, a kodem MMX - po każdym segmencie trzeba poinformować
procesor o konieczności wyczyszczenia stanu rejestrów. No cóż, od razu
chociaż wiemy, że będą jakieś dodatkowe koszty - na usta ciśnie się pytanie
- dlaczego? Odpowiedź nie jest skomplikowana - wielozadaniowe systemy
operacyjne, przełączając zadania, zmieniają kontekst pracy procesora. Przy
każdej takiej operacji trzeba zapamiętać zawartość wszystkich rejestrów
procesora, także i stosu FPU. Gdyby wprowadzić zupełnie nowe rejestry,
musielibyśmy i je zapamiętywać przy przełączaniu - a do tego konieczna jest
modyfikacja odpowiednich części OS. Dzięki wykorzystaniu stosu x87 unikamy
tego typu zmian. Na krótką metę jest to więc w miarę rozsądne
rozwiązanie.
Rejestry nazwano mm0 - mm7. Dostęp do nich jest bezpośredni - nie
ma problemów związanych ze stosem czy inną, bardziej skomplikowaną
organizacją. Jakie typy danych mogą one przechowywać?
- pakowane bajty - osiem liczb 8 bitowych
- pakowane słowa - cztery liczby 16 bitowych
- pakowane słowa podwójne - dwie liczby 32 bitowe
- słowo poczwórne - liczba 64 bitowa
Typy pakowane to po prostu kilka liczb danego typu upakowanych
jedna przy drugiej w rejestrze.
| słowo 1 | słowo 2 | słowo 3 | słowo 4 |
Rzut okiem na oferowane przez MMX typy ujawnia podstawową wadę tego
rozszerzenia: operuje ono wyłącznie na liczbach całkowitych. Musimy
brać to pod uwagę, gdy będziemy rozważać użycie MMX - nie
oznacza to jednak, że od razu trzeba je skreślić. W końcu bardzo
wiele algorytmów operuje na liczbach całkowitych, bądź też daje się w
taki sposób zapisać. Głowa do góry, nie będzie tak źle. Nawet delty
skorzystają ;)
Jedną z głównych zalet intelowskiego rozszerzenia jest ciekawa
odmiana arytmetyki - arytmetyka z nasyceniem (saturacją).
Zwykłe obliczenia, w przypadku nadmiaru, powodują "zawinięcie"
(ang. wrap-around) rejestru:
200 + 100 = 300 mod 256 = 44
(występuje "przebicie" licznika)
Arytmetyka z nasyceniem przyjmuje w takim przypadku maksymalną
wartość oferowaną w ramach danej szerokości rejestru:
200 + 100 = 255
(maksymalna wartość zapisana na 8 bitach)
Tego typu obliczenia są więcej niż przydatne przy zadaniach dotyczących
dźwięku i obrazu - przepełnienia mogą powodować trzaski, a w przypadku
grafiki zasadnicze zmiany kolorów pikseli. MMX jest tu bardzo pomocny - nie
dość, że można w jednym kroku działać na ośmiu 8 bitowych pikselach, to
jeszcze nie trzeba sprawdzać przepełnień i dokonywać korekt, gdyż zajmie się
tym sam procesor.
Zobaczmy, jakie możliwości daje zestaw rozkazów MMX:
-
przede wszystkim operacje arytmetyczne: dodawanie, odejmowanie,
mnożenie, mnożenie z dodawaniem wyników
-
wersje z saturacją - odmiany z uwzględnieniem znaku bądź bez
-
operacje logiczne
-
porównywanie liczb
-
konwersja typów - np. pakowania typów 16 bitowych do postaci 8
bitowej
-
przesunięcia logiczne i arytmetyczne
-
transfer do/z rejestrów
Operacje wykonywane są oczywiście na całej zawartości rejestrów - mamy
więc i odpowiednik przykładowej instrukcji padd - rodzinę paddb,
paddw, paddd (bajty, słowa, słowa podwójne). Co z paddq? Niestety
- arytmetyka na tym formacie danych nie jest możliwa, pozostają działania
logiczne i przesunięcia.
Przyjrzyjmy się, jak można wykorzystać MMX do przyspieszenia liczenia
kilku delt na raz - tym razem 4:
0f 6f 45 f0 movq mm0, [b1, b2, b3, b4]
0f d5 45 f0 pmullw mm0, [b1, b2, b3, b4]
0f 6f 4d d8 movq mm1, [4, 4, 4, 4 ]
0f d5 4d f8 pmullw mm1, [a1, a2, a3, a4]
0f d5 4d e8 pmullw mm1, [c1, c2, c3, c4]
0f f9 c1 psubw mm0, mm1
Jak zwykle, rozpoczynamy od b*b. Ładujemy (MOVe Quadword)
rejestr mm0 wektorem czterech współczynników b - są to liczby
16 bitowe. Mnożenia liczb tego typu dokonujemy przy pomocy polecenia
pmullw (Packed MULtiply Low, Words). Działanie takie
daje 32 bitowy wynik (16b * 16b), zakładamy jednak, że zmieści się on w
dolnych 16 bitach - stąd słowo low w opisie instrukcji. Jeśli
interesuje nas wyższe 16 bitów, skorzystać możemy z wariantu high -
pmulhw. Kolejnym krokiem jest załadowanie rejestru mm1
wektorem składającym się z czwórek. Następnie należy pomnożyć je przez
liczby a oraz c. Odpowiedzialne są za to dwie występujące po
sobie instrukcje pmullw. Zróbmy mały przystanek - zobaczmy, co w tej
chwili zawierają rejestry mm0 oraz mm1.
mm0:
| b1 * b1 | b2 * b2 | b3 * b3 | b4 * b4 |
mm1:
| 4 * a1 * c1 | 4 * a2 * c2 | 4 * a3 * c3 | 4 * a4 * c4 |
Jak widać, by otrzymać w rejestrze mm0 wyniki, wystarczy odjąć
od jego elementów odpowiednie słowa mm1 - to właśnie
zadanie wykonuje ostatnia instrukcja - psubw (Packed
SUBtract, Words)
Wynik:
| b1*b1 - 4*a1*c1 | b2*b2 - 4*a2*c2 | b3*b3 - 4*a3*c3 | b4*b4 - 4*a4*c4 |
Wspaniale - dzięki MMX, przy praktycznie takim samym nakładzie
pracy, możemy wykonać kilka razy więcej obliczeń. Pójdźmy jednak krok
dalej - gdyby teraz z delty wyciągnąć pierwiastek... No tak.
Arytmetyka całkowitoliczbowa. Jednak pozostaje pewien niedosyt...
Cóż, musimy szukać dalej. Może teraz u konkurencji?
3DWhen? 3DNow!

Pierwszy przedstawiciel jednostek 3DNow! (źródło: AMD)
Właśnie - konkurencja. Błędem by było zakładać, że takie firmy jak AMD
czy Cyrix siedziały z założonymi rękoma, obserwując poczynania giganta. Nie,
wszędzie trwały prace - i to nie tylko nad integracją MMX z własnymi
produktami, ale również polepszeniem własności rozszerzenia. Cyrix
rozbudował implementację MMX w swoich procesorach 6x86MX/M-II, dodając kilka
ciekawych rozwiązań - przykładowo część instrukcji potrafiła korzystać z
trzech operandów. Projektanci planowali też wprowadzenie czegoś bardzo
ciekawego - wariantu MMX operującego na liczbach w formacie
zmiennoprzecinkowym. MMXfp - tak miało się to rozwiązanie nazywać - został
jednak porzucony na rzecz propozycji AMD. Pojawił się nowy standard -
pierwsze w świecie x86 rozszerzenie SIMD FP - 3DNow! Stało się ono jednym z
mocniejszych argumentów procesorów serii K6-2.
Zmiany poczynione pomiędzy K6 a K6-2 nie są wielkie (sandpile.org)
Nazwa wskazuje na pole potencjalnego zastosowania - rozrywkowych
aplikacji 3D. Dlaczego rozrywkowych? Przyjrzyjmy się, co nowego wprowadza
3DNow! Po pierwsze - zachowany zostaje model rejestrów MMX. Jest ich tyle
samo, i są tej samej wielkości. Co oznacza to w praktyce? By do jednego 64
bitowego rejestru zmieścić więcej niż jedną liczbę zmiennoprzecinkową,
musimy ograniczyć precyzję do 32 bitowego typu single:
| 32 bity - liczba single | 32 bity - liczba single |
To właśnie stanowi o mniejszej przydatności 3DNow! do szerszej gamy
zastosowań - często pożądana bywa podwójna precyzja. Zaś liczby pojedynczej
precyzji są wystarczające, jeśli chodzi o przekształcenia 3D używane
często w grach. Tak więc oprogramowanie rozrywkowe stało się głównym
celem AMD. Był to spory krok do przodu - MMX od początku powinien był
zawierać wsparcie dla operacji na liczbach zmiennoprzecinkowych, tak jednak
się nie stało. To o tyle ciekawe, że "budżet krzemowy" 3DNow! jest raczej
skromny - procesor K6 od K6-2 różni pół miliona tranzystorów.
Przyjrzyjmy się operacjom oferowanym przez 3DNow!
-
zmiennoprzecinkowe dodawanie, odejmowanie, mnożenie
-
wsparcie dla operacji dzielenia i wyciągania pierwiastka
kwadratowego
-
konwersja typów
-
dodawanie "poziome"
-
wstępne pobieranie danych do obróbki (prefetch)
MMX nie umożliwiał wykonywania dzielenia - 3DNow! daje taką możliwość,
choć nie w jednym kroku. Zależnie od wymaganej precyzji, dzielenie koduje
się 4 bądź 7 instrukcjami. Podobnie jest zresztą z pierwiastkowaniem - tu
również możemy poświęcić precyzję kosztem czasu wykonania. Dzięki omawianym
operacjom ograniczyć można użycie koprocesora x87, a więc związane z tym
przełączanie stanu FPU - chociaż dzięki nowej instrukcji (femms)
może ono być znacznie mniej kosztowne.
Czym jest dodawanie "poziome"? Jest to operacja dodawania wykonana na
liczbach zawartych w jednym rejestrze - okazuje się ona być całkiem
przydatna w wielu sytuacjach.
Wreszcie kilka słów wypada powiedzieć na temat wstępnego pobierania
danych - data prefetching. Jeśli wiemy, że wkrótce wykonywać będziemy
operacje na bloku danych, dobrze jest wcześniej poinformować o tym procesor.
Umożliwiają to instrukcje prefetch/prefetchw zawarte w zestawie
3DNow! W ten sposób liczyć możemy na to, że dane znajdą się w pamięci
podręcznej - pobieranie ich z pamięci głównej może odbywać się "w tle",
podczas przetwarzania poprzedniej iteracji pętli. Ukrywa się w ten sposób
czas sprowadzenia danych, efektywnie zwiększając prędkość działania
programu.
Rzućmy okiem na nieśmiertelne już delty - tym razem dwie za
jednym zamachem:
0f 6f 45 f0 movq mm0, [b1, b2]
0f 0f 45 f0 b4 pfmul mm0, [b1, b2]
0f 6f 4d d8 movq mm1, [4.0, 4.0]
0f 0f 4d f8 b4 pfmul mm1, [a1, a2]
0f 0f 4d e8 b4 pfmul mm1, [c1, c2]
0f 0f c1 9a pfsub mm0, mm1
Nie ma potrzeby dokładniej omawiać kodu - sytuacja odpowiada
praktycznie tej z przykładu dla MMX, tyle że tu przetwarzamy dwie
liczby naraz. Do tego są to liczby zmiennoprzecinkowe - stąd
literka f w nazwie instrukcji.
No tak - delta deltą, ale właściwie dlaczego operacje równoległe
mogą być przydatne w przetwarzaniu grafiki 3D? Otóż bierze to się ze
sposobu, w jaki zwykle opisuje się przekształcenia w przestrzeni
trójwymiarowej. Współrzędne punktu przechowuje się jako wektor o
rozmiarze 4x1, "przepisy" na operacje takie jak obroty, skalowanie czy przesunięcia
zapisać można w postaci macierzy 4x4. Weźmy - przykładowo -
macierz R wymiaru 4x4 opisującą obrót, oraz wektor v,
na którym chcemy dokonać przekształcenia. Wynikowy wektor v'
otrzymamy w wyniku mnożenia:
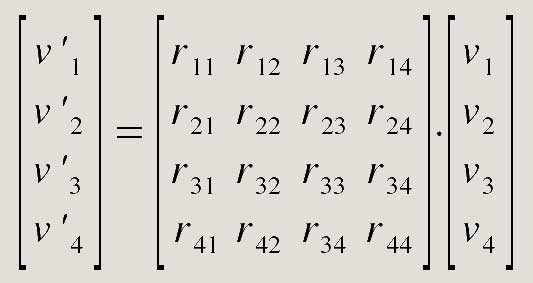
By obliczyć pierwszą współrzędną przekształconego wektora v'1,
czeka nas trochę pracy:
v'1 = r11 * v1 + r12 * v2 + r13 * v3 + r14 * v4
Podobnie liczymy dalsze współrzędne:
v'2 = r21 * v1 + r22 * v2 + r23 * v3 + r24 * v4
v'3 = r31 * v1 + r32 * v2 + r33 * v3 + r34 * v4
v'4 = r41 * v1 + r42 * v2 + r43 * v3 + r44 * v4
Jest to trochę roboty. Szesnaście mnożeń, dwanaście dodawań.
Spróbujmy teraz wykorzystać możliwości 3DNow! Policzymy v'1...
-
rejestr mieści dwie liczby - załadujmy więc r11
i r12 do jednego z nich
-
drugi niech zawiera dwa pierwsze elementy wektora v -
tj. v1 i v2
-
mnożymy oba rejestry przez siebie - otrzymujemy r11
* v1 oraz r12 * v2
-
w drugiej parze rejestrów w analogiczny sposób dochodzimy do r13
* v3 i r14 * v4
-
dodajemy wyniki:
|
r11 * v1 + r13 * v3
|
r12 * v2 + r14 * v4
|
-
musimy teraz dodać obie połówki rejestrów - potrzebujemy tutaj
"poziomego" dodawania:
|
r11 * v1 +
r13 * v3 + r12 * v2 +
r14 * v4
|
r11 * v1 +
r13 * v3 + r12 * v2 +
r14 * v4
|
Gdy przyjrzymy się wynikom, widać, że otrzymaliśmy
v'1! Wykonaliśmy dwa mnożenia, zwykłe i poziome
dodawanie. Całość trzeba oczywiście cztery razy powtórzyć - by poznać
pozostałe elementy v'. W sumie - osiem mnożeń i osiem dodawań, a to
tylko najprostsza możliwa implementacja. Nieźle, prawda? Troszkę uwiera mały
rozmiar rejestru - przydałoby się trochę więcej...
A gdyby mieć więcej miejsca?

Pentium III: witamy Streaming SIMD Extensions!
Jak wyglądałoby przekształcenie, gdybyśmy dysponowali dłuższym
rejestrem - powiedzmy - 128 bitowym? Wystarczy do
przechowania 4 liczb pojedynczej precyzji - akurat wiersz czy
kolumna macierzy. Dla odmiany załóżmy, że tym razem nie dysponujemy
dodawaniem poziomym. Co więc można zrobić? Zauważmy, że pierwszym
krokiem we wszystkich wzorach jest wymnożenie r_1
przez v1. Podobnie - mnożymy elementy drugiej
kolumny przez v2, etc. Jaka z tego korzyść?
Zbierzmy elementy pierwszej kolumny w wektorze, drugi wypełnijmy
wartościami v1:
[ r11 r21 r31 r41
], [ v1 v1 v1 v1 ]
Pozostaje pomnożyć odpowiednie elementy obu wektorów, i... jedna czwarta
pracy za nami - dzięki zastosowaniu podejścia SIMD, jednym ruchem wykonujemy
cztery mnożenia odpowiadające pierwszym mnożeniom rozpisanych wcześniej
wierszy!
[ r12 r22 r32 r42
], [ v2 v2 v2 v2 ]
[ r13 r23 r33 r43
], [ v3 v3 v3 v3 ]
[ r14 r24 r34 r44
], [ v4 v4 v4 v4 ]
Po kolejnych trzech operacjach mamy składowe wyniku - wystarczy je tylko
dodać do siebie. Użyliśmy czterech mnożeń SIMD, oraz trzech dodawań.
Musieliśmy za to podać macierz w postaci kolumn, i wypełniać drugi wektor
powielanymi elementami.
Tym samym zobaczyliśmy, w jaki sposób działa kolejne rozszerzenie -
Streaming SIMD Extensions - SSE. Znane było początkowo jako
Katmai New Instructions - KNI - a to ze względu na premierę
wraz z pierwszymi procesorami Pentium III, o kodowej nazwie Katmai.
Od tego czasu obecne jest w kolejnych produktach Intela (w Celeronach SSE
obsługiwane jest począwszy od modeli opartych o jądro Coppermine). Po
stronie AMD nowy zestaw instrukcji ochrzczony został mianem 3DNow!
Professional - i pojawił się w pierwszych Athlonach XP -
Palomino. Częściowo zgodne z SSE są też starsze procesory Athlon -
niestety, nie dotyczy to operacji zmiennoprzecinkowych.
SSE wprowadza spore zmiany - przede wszystkim nowe, szerokie rejestry.
Zrywa w ten sposób ze zgodnością ze starszymi systemami operacyjnymi -
przykład zachowawczej konstrukcji MMX i tego konsekwencji pokazuje, że był
to dobry wybór. Nowych rejestrów jest osiem, mają po 128 bitów - dokładnie
tyle, ile potrzebne jest do przechowania 4 liczb single. Rejestry
nazwano xmm0 - xmm7. Podobnie jak w przypadku rejestrów MMX,
mamy do nich bezpośredni dostęp. Jedyny wprowadzony typ danych to właśnie
liczby pojedynczej precyzji.
SSE wykonuje obliczenia w dwóch trybach:
-
packed - działania przeprowadzane są na wszystkich 4
polach rejestru (np. addps)
-
scalar - działania przeprowadzane są na jednej liczbie
(addss)
Jaki ma sens wprowadzenie drugiej kategorii instrukcji? Nie zawsze
chcemy działań równoległych, a szkoda marnować zasoby na niepotrzebne
obliczenia. Szkoda też odwoływać się do rozkazów x87, po to tylko, by
wykonać kilka operacji.
Jakie możliwości daje SSE? Podzielmy je na kategorie:
-
operacje arytmetyczne - nie tylko dodawanie, odejmowanie i
mnożenie, ale też dzielenie, wyciąganie pierwiastka, szukanie
minimum i maksimum
-
odwracanie liczb i ich pierwiastków
-
wykonywanie porównań
-
operacje logiczne
-
konwersję formatów
-
zamianę pól wewnątrz rejestru
-
transfer z/do rejestrów 128 bitowych
-
wstępne pobieranie danych, zapis z pominięciem cache
-
rozszerzenia całkowitoliczbowego MMX - makisma i minima, etc. -
zasadniczo zgodne z rozszerzeniami AMD
SSE to pokaźny zestaw instrukcji - podobnie jak 3DNow!, zawiera też
dodatkowi wspomagające przetwarzanie dużych bloków danych. Poza odczytem,
można również wymusić zapis danych z ominięciem pamięci podręcznej. Stąd
zresztą słowo Streaming w nazwie rozszerzenia
- chodzi o wskazanie przydatności SSE w przetwarzaniu mediów
strumieniowych.
Wydaje się, że w starciu z SSE zestaw 3DNow! nie ma żadnych szans.
Dysponuje przecież większymi rejestrami, potrzebuje więc mniej operacji...
Owszem, lecz nikt nie daje nam gwarancji wykonywania działań w jednym cyklu
- tak naprawdę rozkazy dzielone są na dwie 64 bitowe połowy. Teoretyczna
przepustowość obu rozwiązań jest więc podobna. Niewątpliwie kod SSE może być
bardziej zwarty. Szkoda tylko, że nie ma odpowiednika instrukcji poziomego
dodawania.
Nadszedł więc chyba czas na... delty, a jak. Znów liczby
zmiennoprzecinkowe, cztery za jednym zamachem:
0f 28 45 28 movaps xmm0, [b1, b2, b3, b4]
0f 59 45 28 mulps xmm0, [b1, b2, b3, b4]
0f 28 4d d8 movaps xmm1, [4.0, 4.0, 4.0, 4.0]
0f 59 4d 18 mulps xmm1, [a1, a2, a3, a4]
0f 59 4d 38 mulps xmm1, [c1, c2, c3, c4]
0f 5c c1 subps xmm0, xmm1
Także i ten fragment nie wymaga zbyt obszernego komentarza - widzieliśmy
już tyle wersji liczenia delty, że bez problemu rozróżniamy poszczególne
operacje. Zwróćmy uwagę na wykorzystanie wariantów packed -
zakończonych ps. Rejestry ładowane są przy pomocy movaps -
zakłada to wyrównanie danych w pamięci do granicy 16 bajtów (MOVe
Aligned).
Czego brakuje? Precyzji, precyzji...
Wszystkie omówione do tej pory
dodatkowe zestawy instrukcji dobrze spełniają swoje zadanie. Szkoda
tylko, że działają wyłącznie na danych pojedynczej precyzji. Dobrze
by było, gdyby rozszerzyć SSE o działania na liczbach typu double.
Stało się to podstawą konstrukcji kolejnej ewolucji rozszerzenia -
SSE-2. Na rynek trafiło ono wraz z procesorem Pentium 4. Można
odnieść wrażenie, że celowo "przycięto" jednostkę x87
celem wypromowania SSE-2. Trzeba przyznać, że faktycznie wraz z
szerszym przyjęciem SSE-2 rozpoczął się proces odchodzenia od
używania klasycznego koprocesora. Bezpośredni dostęp do rejestrów,
operacje skalarne, a teraz jeszcze podwójna precyzja w SSE-2 -
to wystarczające argumenty. Wciąż jednak pozostają operacje, których
nie wykonamy przy użyciu jednostek SSE/SSE-2 (np. funkcje sinus
czy cosinus).

SSE-2 pozwala uratować honor Pentium 4
Co nowego wnosi SSE-2 do modelu rejestrów? W wykonaniu firmy Intel -
niewiele. Wprowadzony został nowy typ danych - dwie spakowane, 64 bitowe
liczby double. Ilość rejestrów pozostała bez zmian. Dopiero
implementacja SSE-2 będąca częścią AMD64 (EM64T) dodaje osiem kolejnych -
xmm8 do xmm15.
Nie będzie prawdą stwierdzenie, jakoby SSE-2 ograniczać się miało do
wprowadzenia operacji na nowym typie danych. SSE-2 to znacznie więcej.
Przede wszystkim - instrukcje MMX mogą teraz operować na rejestrach
xmm - SSE-2 to jakby MMX-128. Stąd pojawiające się co jakiś czas
wskazówki, by odchodzić od zestawu MMX na rzecz SSE-2 - osiąga się podobną
funkcjonalność, ale operuje na 128 bitach na raz. Wraz z SSE-2 maleje więc
znaczenie pierwszego z rozszerzeń SIMD x86.
Dochodzi do tego oczywiście zestaw rozkazów konwersji typów czy
kopiowania danych.
Naturalnie, opis nie będzie kompletny bez kilku delt, prawda? ;)
Może najpierw wprowadzimy podwójną precyzję:
66 0f 28 45 28 movapd xmm0, [b1, b2]
66 0f 59 45 28 mulpd xmm0, [b1, b2]
66 0f 28 4d d8 movapd xmm1, [4.0, 4.0]
66 0f 59 4d 18 mulpd xmm1, [a1, a2]
66 0f 59 4d 38 mulpd xmm1, [c1, c2]
66 0f 5c c1 subpd xmm0, xmm1
Zmianą w stosunku do SSE jest pojawienie się końcówki d - od
specyfikacji precyzji - double. Rejestr mieści teraz dwie liczby,
poza tym kod jest praktycznie identyczny.
Mowa była o wykorzystaniu SSE-2 jako 128 bitowej odmiany MMX. Umożliwi to
jednorazowe policzenie ośmiu 16 bitowych wyników:
0f 28 45 28 movaps xmm0, [b1, b2, b3, b4, b5, b6, b7, b8]
66 0f d5 45 28 pmullw xmm0, [b1, b2, b3, b4, b5, b6, b7, b8]
0f 28 4d d8 movaps xmm1, [4, 4, 4, 4, 4, 4, 4, 4]
66 0f d5 4d 18 pmullw xmm1, [a1, a2, a3, a4, a5, a6, a7, a8]
66 0f d5 4d 38 pmullw xmm1, [c1, c2, c3, c4, c5, c6, c7, c8]
66 0f f9 c1 psubw xmm0, xmm1
Porównajmy kod z odpowiednikiem MMX - różnią się tylko odwołania do
rejestrów (no i oczywiście sposób ich ładowania).
Można już odetchnąć z ulgą - to ostatnie pojawienie się delt w tym tekście ;)
Co kryje w sobie Prescott?
Jak Intel mógł nazwać dodatkowe instrukcje zaszyte w jądrze Prescott?
Kodowe określenie - PNI - Prescott New Instructions, zmienione
zostało na SSE-3. To w sumie kilkanaście nowych rozkazów, dotyczących
różnych obszarów działania procesora. Podzielimy je na grupy - rozkazy FPU,
rozszerzenia SSE-2, oraz dodatkowe wsparcie dla technologii Hyper
Threading.
SSE-3 dodaje nową instrukcję FPU (tak, rozszerzony zostaje stary zestaw
instrukcji x87). fisttp (Fp Integer Store with Truncation and
Pop) przekształca liczbę zmiennoprzecinkową na jej całkowitą
postać - obcinając część ułamkową. Różni się tym od starszego rozkazu
fistp, który potrafi skorzystać z innych metod zaokrąglania
liczb.
Instrukcje SSE-2 uzupełnione zostały kilkoma pożytecznymi dodatkami.
Rodzina intelowskich rozszerzeń doczekała się operacji poziomych - dodawania
(haddps, haddpd) oraz odejmowania (hsubps,
hsubpd).
Dostępne są też mieszane operacje dodawania/odejmowania elementów
rejestrów - addsubps, addsubpd. Instrukcje te okazują się być
szczególnie przydatne przy mnożeniu liczb zespolonych. Także i w tym
przypadku Intel dopiero dogania konkurencję - podobne polecenie
(pfpnacc) AMD udostępniło użytkownikom wraz z rozszerzonym na
potrzeby Athlona Enhanced 3DNow! Również z myślą o algorytmach liczb
zespolonych dodano rozkazy przesunięć z powielaniem argumentów (movddup -
MOVe Double and DUPlicate, movshdup - MOVe Single High and DUPlicate,
movsldup - MOVe Single Low and DUPlicate).
Rozkaz lddqu ładuje niewyrównane do granicy 16 bajtów dane do
wybranego rejestru xmm. W porównaniu z dostępnymi do tej pory
instrukcjami - przy odwołaniach przechodzących przez granice linii pamięci
cache, lddqu może znacząco przyspieszyć działanie programu. Intel
poleca użycie tej instrukcji przy projektowaniu oprogramowania kodującego
wideo - występuje w nim sporo niewyrównanych odwołań.
Pozostają dwie nowości dotyczące HT - monitor oraz
mwait. monitor ustala obszar pamięci, który w
specjalnym trybie pracy monitorowany będzie na wystąpienie pewnych
operacji (np. zapisu). By procesor wszedł we wspomniany tryb, użyć
należy drugiego rozkazu - mwait. Procesor zajmuje się
wtedy monitorowaniem wybranego wcześniej obszaru - normalnie to
program musiałby w pętli sprawdzać, czy operacja zapisu została już
wykonana, czy może jeszcze nie. Oszczędzamy w ten sposób jednostki
wykonawcze CPU, daje to też pozytywny efekt jeśli chodzi o konsumpcję
energii. W przypadku Prescotta to dosyć ważne ;)
Wszystko? Gdzieżby, może większość...
Tak oto docieramy do końca podróży przez dodatki do architektury x86.
Powtórzmy, gdzie się zatrzymywaliśmy. Sprawdziliśmy, jak wyglądają
klasyczne operacje wykonywane przez CPU. By nie straszne nam były
ułamki, wpadliśmy na moment z wizytą do sąsiedniej krainy x87.
Później rozpoczęliśmy eksplorację MMX, zaraz potem 3DNow!, nie obyło
się też bez kilku odmian SSE. Poznaliśmy, w jaki sposób rozszerzenia
te przyspieszać mogą popularne obliczenia przekształceń 3D, przy
okazji wiemy też, jak w miarę szybko policzyć kilka wyznaczników
trójmianu ;) Mam nadzieję, że ciekawość Czytelników została w pewnym
chociaż stopniu zaspokojona.
